Remember since y equals x for all values we say the equation of this graph is y=x

What about a steeper or less steep hill ?

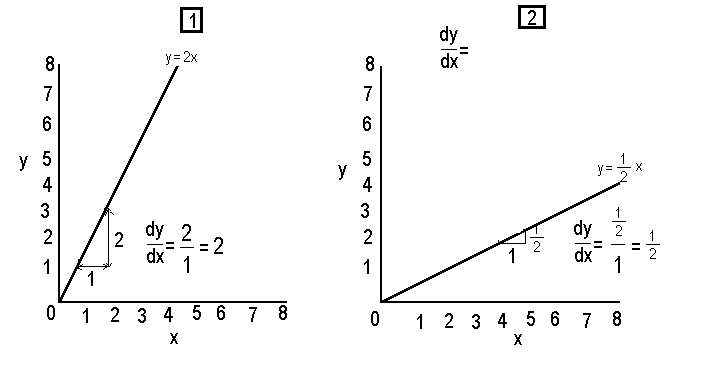
Here in the first graph y= 2x . If we take one unit or meter along the x axis anywhere we see that y increases by 2 units or meters . So the gradient or steepness is 2 meter for every meter . In maths we call the gradient a differential . In mathematics we write the rate of change of y with respect ot x as dy/dx (pronounces as dy by dx ) . If y = 3x the differential ie increase in y for each unit of increase in x would be 3.. Similarly for y = half x we get dy by dx as half as in graph 2 above.

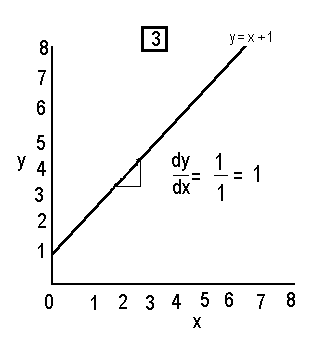
The equation is y=x + 1 . Here we see that the gradient or dy/dx is still 1 . So we can generalise further that when y= ax + k where a and k are constants and do not change that dy by dx is still a .

The next graph 4 below may look complicated but if we break it down it will become easy to understand. What is happening here is that we climb till we get to the top of the hill and then thankfully walk on a flat top for about 4 metres and then walk downhill. Lets pick three sites A , B and C and see what happens to the gradient - dy by dx at each.

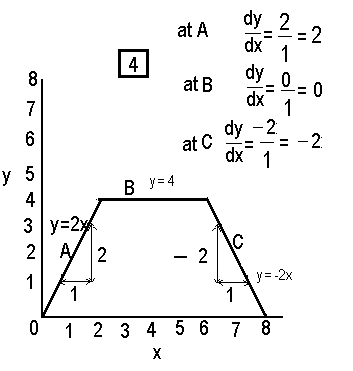
At A it is uphill and since y increases by 2 for each increase in x the gradient is 2. At B y increases by zero when increases by one so the gradient is 0 as it is of any horizonatal line . At C y goes from 3 to 2 when x goes from 6.5 to 7.5 ie it decreases or is -2 , so the gradient or dy by dx is -2 .

The equations of the lines also changes from y= 2x to y = 4 to y = -2x

If we look at out three equations and their gradients we see that when y=x gradient or dy/dx = 1 , when y=2x or 2x +1 gradient or dy/dx =2 , when y = 3 dy/dx is 3 ...We can generalise that when y =ax the gradient must be a .

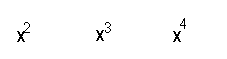
Supposing the hill obeyed a law y= xexp2 then the graph would look like this

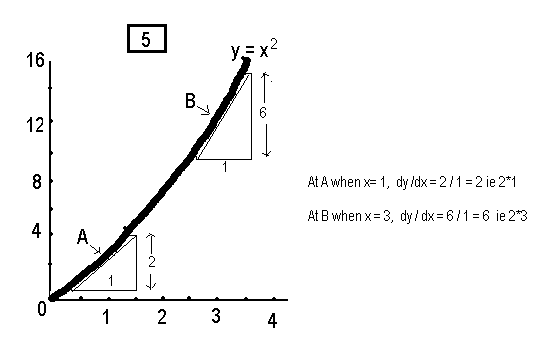
We could measure its steepness anywhere by drawing a line for eg at A and B . The gradient at A when x = 1 or dy/dx is from the graph 2 ( vaule of x times 2 ) and at B when x = 3 is 6 ( ie value of x =3 times 2) . In fact the gradient at any point is 2x .

We can draw more graphs and will find that the result is as follows .

for y = x exp 2 + 3 , dy/dx is 2x ; for y = x exp 3 , dy /dx is 3xexp2

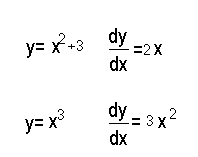
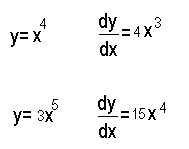
In fact we can generalise that when y = ax expn + k where a and k are constants then the gradient or dy by dx is n*a*xexp(n-1)

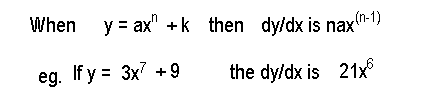
This is an incredibly useful formula as it saves us
from having to draw incredibly complicated graphs ! More important many important events in nature follow the law of curves so we can find the rate of change by using this differential formula.

What is the use of all this one may ask ! Consider a train starting from a station and lets plot its distance on the y vertical axis but label it as s , and the time along the x axis in seconds as in graph 4 below.

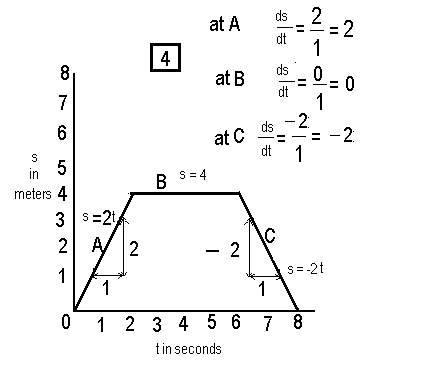At A when t increases by one second the distance goes up by 2 meters so the gradient or steepness is 2 :1 or 2 . But by definiton the speed of something is its change in one second ( or one unit of time ) and so the speed is 2 meters per second .At B the train is stopped so there is no change in distance from the station and the change is 0 , the speed is also 0 . At C can you guess whats happening ? since the distance is decreasing the train must be returning ! So its distance from the station is decreasing so the change is one second of distance from 0 is -2 , so the speed ( as measured away from the station is minus 2 ). So the speed is given always by the differential of the distance . So if we donate this as v , we can say v= ds/dt or d/dt ( s) ie the same thing , called the differential of distance with respect to time .

Similarly acceleration is defined as the change of velocity ( speed ) with respect to time so a ( acc) = dv/dt. Since v itself is a differential of s the distance we can say that acc a is the differential of the differential of s ie

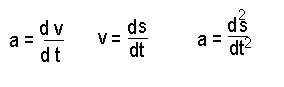
If the acceleration itself was changing with respect to time then we could differentiate that too da/dt .

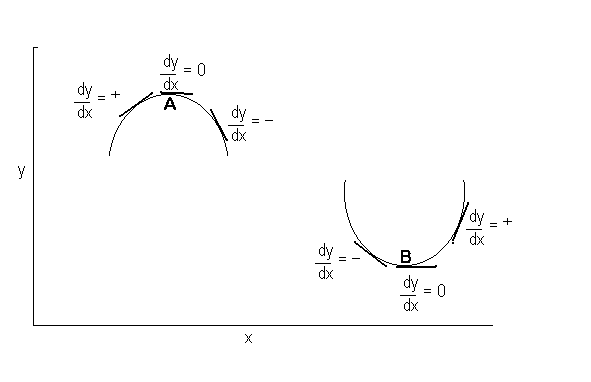
Similarly at B the gradient goes from negative to zero to positive as x increases for a minimum point ie it is increasing . We can plot the changes of dy by dx just before and after A and B in the graph below .

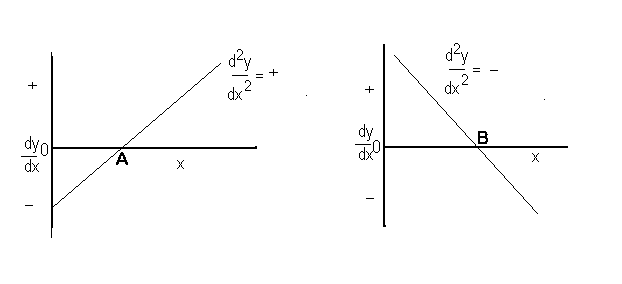
Since d2y by dx2 is the rate of change of dy by dx with respect to x ie it is the gradient of dy by dx we can see that for a maximum point dy by dx must be zero , and d2y by dx2 negative and for a minimum point dy by dx must be zero and d2y by dx2 must be positive.

for example find the max and min point of xexp Supposing we measure that a rocket changes its distance according to this complicated formula .

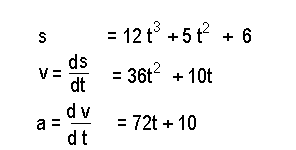
We can instantly tell that the distance after say 3 seconds is 324+45 + 6 = 375meters ; that the speed or velocity is 324+30 = 354 meters per second and that it is accelerating at 216+10 = 226 meters per second per second.

Computers can do these calculations very fast and without the knowledge of this equation space travel may not have been possible .

In the next lesson we will have a look at the reverse of differentiation which is called ......

x+y+z = 12 equation A ; x-y-z = -2 equation B ; x+2y+z=16 equation C.

What we have to do is to look at A and leave just x on this side

So x = 12-y-z

We can now put this value of x in B

(12-y-z) -y -z = -2 and opening the bracket 12-y-z-y-z = -2 so 12 - 2y - 2z = -2 so 12 +2= 2y+2z so 14 = 2y+2z and dividing each side by 2 we get 7= y+z equation D

So y = 7-z

Putting the value of x and of in equation C we get

12- y-z +2y+z=16

so y =4 equation E

Put this value of y in D and we get 4= 7-z so z = 3 and putting y and z in equation A we get x+4+3= 12 so x is 5

Check by putting x y and z in equation B 5-4-3 = -2 and this is correct so x=5 , y=4 and z=3 is correct. Luckily in equation E z cancelled out but if it had not yoy would have got another equation with a z term and this with D would have formed 2 equations with two unknowns and would have been solved as shown in lesson 1.

Solve the following 4+9 (2+1) + 3y - 3 of 2 + ( y + 2y) -6/2 +5*2 + yexp 2 . Note OF is the same as * . Answer in the next lesson .